La derivada de una función en un valor de entrada dado que describe la mejor aproximación lineal de una función cerca del valor de entrada. Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente en la gráfica de la función en dicho punto. En dimensiones más elevadas, la derivada de una función en un punto es la transformación lineal que más se aproxima a la función en valores cercanos de ese punto. Algo estrechamente relacionado es el diferencial de una función.
El proceso de encontrar una derivada es llamado diferenciación. El teorema fundamental del cálculo dice que la diferenciación es el proceso inverso de la integración en funciones continuas.

Historia de la derivada
Los problemas típicos que dieron origen al cálculo infinitesimal, comenzaron a plantearse en la época clásica de la antigua Grecia (siglo III a.c), pero no se encontraron métodos sistemáticos de resolución hasta veinte siglos después (en el siglo XVII por obra de Isaac Newton y Gottfried Leibniz).
En lo que atañe a las derivadas existen dos conceptos de tipo geométrico que le dieron origen:
- El problema de la tangente a una curva (Apolonio de Perge)
- El problema de los extremos: máximos y mínimos (Pierre de Fermat)
[editar] Siglo XVII
Los matemáticos perdieron el miedo que los griegos le habían tenido a los infinitos: Johannes Kepler y Bonaventura Cavalieri fueron los primeros en usarlos, empezaron a andar un camino que llevaría en medio siglo al descubrimiento del cálculo infinitesimal.A mediados del siglo XVII, las cantidades infinitesimales fueron cada vez mas usadas para resolver problemas de cálculos de tangentes, áreas, volúmenes; los primeros darían origen al cálculo diferencial, los otros al integral.
[editar] Newton y Leibniz
A finales del siglo XVII sintetizaron en dos conceptos, métodos usados por sus predecesores los que hoy llamamos "derivadas" e "integrales". Desarrollaron reglas para manipular las derivadas (reglas de derivación) y mostraron que ambos conceptos eran inversos (teorema fundamental del cálculo).Newton desarrolló en Cambridge su propio método para el cálculo de tangentes. En 1665 encontró un algoritmo para derivar funciones algebraicas que coincidía con el descubierto por Fermat. A finales de 1665 se dedicó a reestructurar las bases de su cálculo, intentando desligarse de los infinitesimales, e introdujo el concepto de fluxión, que para él era la velocidad con la que una variable "fluye"(varía) con el tiempo.
Leibniz, por su parte, descubrió y comenzó a desarrollar el cálculo diferencial en 1675. Fue el primero en publicar los mismos resultados que Newton descubriera 10 años antes. En su investigación conservó un carácter geométrico y trató a la derivada como un cociente incremental y no como una velocidad. Fue quizás el mayor inventor de símbolos matemáticos. A él se deben los nombres de: cálculo diferencial y cálculo integral, así como los símbolos
 y el símbolo de la integral
y el símbolo de la integral 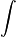 .
.[editar] Conceptos y aplicaciones
El concepto de derivada es uno de los dos conceptos centrales del cálculo infinitesimal. El otro concepto es la "antiderivada" o integral; ambos están relacionados por el teorema fundamental del cálculo. A su vez, los dos conceptos centrales del cálculo están basados en el concepto de límite, el cual separa las matemáticas previas, como el Álgebra, la Trigonometría o la Geometría Analítica, del Cálculo. Quizá la derivada es el concepto más importante del Cálculo Infinitesimal.La derivada es un concepto que tiene variadas aplicaciones. Se aplica en aquellos casos donde es necesario medir la rapidez con que se produce el cambio de una magnitud o situación. Es una herramienta de cálculo fundamental en los estudios de Física, Química y Biología, o en ciencias sociales como la Economía y la Sociología. Por ejemplo, cuando se refiere a la gráfica de dos dimensiones de f, se considera la derivada como la pendiente de la recta tangente del gráfico en el punto x. Se puede aproximar la pendiente de esta tangente como el límite cuando la distancia entre los dos puntos que determinan una recta secante tiende a cero, es decir, se transforma la recta secante en una recta tangente. Con esta interpretación, pueden determinarse muchas propiedades geométricas de los gráficos de funciones, tales como concavidad o convexidad.
Algunas funciones no tienen derivada en todos o en alguno de sus puntos. Por ejemplo, una función no tiene derivada en los puntos en que se tiene una tangente vertical, una discontinuidad o un punto anguloso. Afortunadamente, gran cantidad de las funciones que se consideran en las aplicaciones son continuas y su gráfica es una curva suave, por lo que es susceptible de derivación.
Las funciones que son diferenciables (derivables si se habla en una sola variable), son aproximables linealmente.
[editar] Introducción geométrica a las derivadas
Supongamos que tenemos una función y la llamamos . La derivada de
. La derivada de  es otra función que llamaremos
es otra función que llamaremos  .
.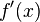 representa la pendiente de la recta tangente a la gráfica de
representa la pendiente de la recta tangente a la gráfica de  en el punto
en el punto  .
.En términos geométricos, esta pendiente
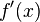 es "la inclinación" de la línea recta que pasa justo por encima del punto
es "la inclinación" de la línea recta que pasa justo por encima del punto 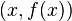 y que es tangente a la gráfica de
y que es tangente a la gráfica de  .
.Al identificar dos puntos muy cercanos en la gráfica y al unirlos mediante una línea recta, una pendiente queda visualizada. Cuanto más cercanos sean los dos puntos que se unen por medio de la recta, la recta se parece más a una recta tangente a la gráfica y su pendiente se parece más a la pendiente de una recta tangente.
Notamos que esta pendiente coincide con la rapidez con que aumenta el valor de la función en cada punto. Dicho de otra manera, si la pendiente en un punto es muy grande, entonces el valor de la función en ese punto crece muy deprisa; si la pendiente es muy pequeña, entonces el valor de la función crece muy despacio en ese punto.
Es decir, tanto la pendiente de la recta tangente como la rapidez de crecimiento en un punto
 de una función
de una función  está dado por
está dado por 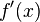 .
.No todas las funciones poseen derivada. Desde el punto de vista geométrico esto se puede deber a varios motivos. Por ejemplo hay funciones donde se da el caso de que por un mismo punto pasan muchas rectas tangentes(por ejemplo la función valor absoluto en el punto 0) y no es posible definir de manera única la pendiente a la recta tangente. También se da el caso de que no se puede definir la pendiente a una recta tangente en una función que no es continua. Incluso hay funciones donde cualquier recta que pase por uno de sus puntos interseca en una infinidad de puntos muy cercanos y por tanto no hay recta tangente.
Las funciones que poseen derivada se llaman diferenciables.
Conocer la derivada de una función diferenciable por lo general resulta una tarea sencilla utilizando las técnicas de derivación desarrolladas por Gottfried Leibniz e Isaac Newton, las cuales permiten conocer las derivadas de muchas de las funciones de interés frecuente o bien, simplificar el trabajo para encontrar derivadas menos comunes.
[editar] Condiciones de continuidad de una función
Una función continua es aquella cuya regla de correspondencia asigna incrementos pequeños en la variable dependiente a pequeños incrementos de los elementos del dominio de dicha función, es decir, , y usando la expresión Δy + y = f(Δx + x), queda
, y usando la expresión Δy + y = f(Δx + x), queda  donde en este caso, f(x) = y. Ello quiere decir que
donde en este caso, f(x) = y. Ello quiere decir que 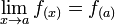 , y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con
, y si este último límite existe significa en consecuencia por un teorema de límites (un límite existe si y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con es continua en el punto a.
es continua en el punto a.[editar] Condición no recíproca
La relación no funciona a la inversa: el que una función sea continua no garantiza su derivabilidad. Es posible que los límites laterales sean equivalentes pero las derivadas laterales no; en este caso la función presenta un punto anguloso en dicho punto.Un ejemplo puede ser la función valor absoluto (también llamada módulo) en el punto
 . Dicha función es equivalente a la función partida
. Dicha función es equivalente a la función partida 
Para valores infinitamente cercanos a 0, por ambas ramas, el resultado tiende a 0. Y el resultado en el punto 0 es también 0, por lo tanto es continua. Sin embargo, las derivadas resultan

Cuando
 vale 0, las derivadas laterales dan resultados diferentes. Por lo tanto, no existe derivada en el punto, a pesar de que sea continuo.
vale 0, las derivadas laterales dan resultados diferentes. Por lo tanto, no existe derivada en el punto, a pesar de que sea continuo.De manera informal, si el gráfico de la función tiene puntas agudas, se interrumpe o tiene saltos, no es derivable.
[editar] Definición analítica de derivada como un límite
En terminología clásica, diferenciación manifiesta el coeficiente en que una cantidad cambia a consecuencia de un cambio en otra cantidad
cambia a consecuencia de un cambio en otra cantidad  .
.En matemáticas coeficiente es un factor multiplicativo que pertenece a cierto objeto como una variable, un vector unitario, una función base, etc.
En física coeficiente es una expresión numérica que mediante alguna fórmula determina las características o propiedades de un cuerpo.
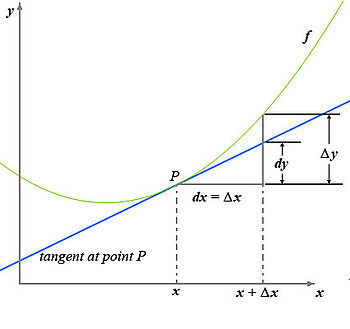
En nuestro caso, observando la gráfica de la derecha, el coeficiente del que hablamos vendría representado en el punto
 de la función por el resultado de la división representada por la relación
de la función por el resultado de la división representada por la relación  , que como puede comprobarse en la gráfica, es un valor que se mantiene constante a lo largo de la línea recta azul que representa la tangente en el punto
, que como puede comprobarse en la gráfica, es un valor que se mantiene constante a lo largo de la línea recta azul que representa la tangente en el punto  de la función. Esto es fácil de entender puesto que el triangulo rectángulo formado en la gráfica con vértice en el punto
de la función. Esto es fácil de entender puesto que el triangulo rectángulo formado en la gráfica con vértice en el punto  , por mucho que lo dibujemos más grande, al ser una figura proporcional el resultado de
, por mucho que lo dibujemos más grande, al ser una figura proporcional el resultado de 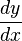 es siempre el mismo.
es siempre el mismo.Esta noción constituye la aproximación más veloz a la derivada, puesto que el acercamiento a la pendiente de la recta tangente es tanto por la derecha como por la izquierda de manera simultánea.
En particular, se tiene que la derivada de la función en el punto
 se define como sigue:
se define como sigue: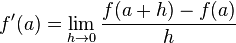 ,
,
Aunque podrían calcularse todas las derivadas empleando la definición de derivada como un límite, existen reglas bien establecidas, conocidas como teoremas para el cálculo de derivadas, las cuales permiten calcular la derivada de muchas funciones de acuerdo a su forma sin tener que calcular forzosamente el límite. Tales reglas son consecuencia directa de la definición de derivada y de reglas previas, como puede apreciarse en todo buen texto de cálculo infinitesimal.
También puede definirse alternativamente la derivada de una función en cualquier punto de su dominio de la siguiente manera:
 ,
,
 . El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.
. El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.No obstante su aparente diferencia, el cálculo de la derivada por definición con cualquiera de los límites anteriormente expresados, proporciona siempre el mismo resultado.
El conocimiento de todas las expresiones anteriores y su significado representan el acercamiento epistémico más completo posible en torno a la definición de derivada, y con ello, al aspecto esencial del cálculo diferencial.
[editar] Notación
Existen diversas formas para nombrar a la derivada. Si f es una función, se escribe la derivada de la función respecto al valor
respecto al valor  en varios modos:
en varios modos: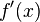 {Notación de Lagrange}
{Notación de Lagrange}
se lee "
 sub
sub  de
de  ", y los símbolos D y d deben entenderse como operadores.
", y los símbolos D y d deben entenderse como operadores. { Notación de Newton}
{ Notación de Newton}
 " o "
" o " punto". Actualmente está en desuso en Matemáticas puras, sin embargo se sigue usando en áreas de la física como la mecánica, donde otras notaciones de la derivada se pueden confundir con la notación de velocidad relativa. Se usa para definir la derivada temporal de una variable.
punto". Actualmente está en desuso en Matemáticas puras, sin embargo se sigue usando en áreas de la física como la mecánica, donde otras notaciones de la derivada se pueden confundir con la notación de velocidad relativa. Se usa para definir la derivada temporal de una variable. ,
,  ó
ó  {Notación de Leibniz}
{Notación de Leibniz}
 (
( ó
ó  de
de  ) con respecto a
) con respecto a  ". Esta notación tiene la ventaja de sugerir a la derivada de una función con respecto a otra como un cociente de diferenciales.
". Esta notación tiene la ventaja de sugerir a la derivada de una función con respecto a otra como un cociente de diferenciales.La notación más simple para diferenciación, en uso actual, es debida a Lagrange. Para identificar las derivadas de
 en el punto a, se escribe:
en el punto a, se escribe: para la primera derivada,
para la primera derivada, para la segunda derivada,
para la segunda derivada, para la tercera derivada,
para la tercera derivada, para la enésima derivada (n > 3). (También se pueden usar números romanos).
para la enésima derivada (n > 3). (También se pueden usar números romanos).
 en
en  , se escribe
, se escribe  . De modo parecido, para la segunda derivada de
. De modo parecido, para la segunda derivada de  en
en  , se escribe
, se escribe  , y así sucesivamente.
, y así sucesivamente.La otra notación común para la diferenciación es debida a Leibniz. Para la función derivada de
 , se escribe:
, se escribe: , se puede escribir la derivada como
, se puede escribir la derivada como o
o 
 o de y respectivamente. Históricamente, esto viene del hecho que, por ejemplo, la tercera derivada es
o de y respectivamente. Históricamente, esto viene del hecho que, por ejemplo, la tercera derivada esLa notación de Newton para la diferenciación respecto al tiempo, era poner un punto arriba del nombre de la función:
Esta notación de Newton se usa principalmente en mecánica, normalmente para derivadas de tiempo tales comos velocidad y aceleración, y en teoría de ecuaciones diferenciales ordinarias. Usualmente solo se usa para las primeras y segundas derivadas.
[editar] Diferenciabilidad
Una función con dominio en un subconjunto de los reales es diferenciable en un punto x si su derivada existe en ese punto; una función es diferenciable en un intervalo si es diferenciable en todos los puntos del intervalo.Si una función es diferenciable en un punto x, la función es continua en ese punto. Sin embargo, una función continua en x, puede no ser diferenciable en dicho punto. En otras palabras, diferenciabilidad implica continuidad, pero no su recíproco.
La derivada de una función diferenciable puede ser, a su vez, diferenciable. La derivada de una primera derivada se llama derivada segunda. De un modo parecido. La derivada de una derivada segunda es la derivada tercera, y así sucesivamente. Esto también recibe el nombre de derivación sucesiva o derivadas de orden superior.
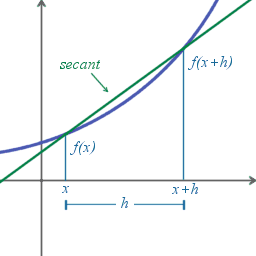
[editar] Cociente de diferencias de Newton
La derivada de una función es la pendiente geométrica de la línea tangente del gráfico de
es la pendiente geométrica de la línea tangente del gráfico de  en
en  . Sin el concepto que se va a definir, no es posible encontrar directamente la pendiente de la línea tangente a una función dada, porque solamente se conoce un punto en la línea tangente:
. Sin el concepto que se va a definir, no es posible encontrar directamente la pendiente de la línea tangente a una función dada, porque solamente se conoce un punto en la línea tangente: 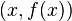 . La idea es aproximar la línea tangente con múltiples líneas secantes que tienen distancias progresivamente más pequeñas entre los dos puntos que cruzan. Cuando se toma el límite de las pendientes de las líneas secantes de esta progresión, se consigue la pendiente de la línea tangente. Se define, pues, la derivada tomando el límite de la pendiente de las líneas secantes, al acercarlas a la línea tangente.
. La idea es aproximar la línea tangente con múltiples líneas secantes que tienen distancias progresivamente más pequeñas entre los dos puntos que cruzan. Cuando se toma el límite de las pendientes de las líneas secantes de esta progresión, se consigue la pendiente de la línea tangente. Se define, pues, la derivada tomando el límite de la pendiente de las líneas secantes, al acercarlas a la línea tangente.Para encontrar las pendientes de las líneas secantes próximas, se elige un número
 relativamente pequeño.
relativamente pequeño.  representa un cambio relativamente pequeño en
representa un cambio relativamente pequeño en  , el cual puede ser positivo o negativo. La pendiente de la línea que cruza los dos puntos
, el cual puede ser positivo o negativo. La pendiente de la línea que cruza los dos puntos 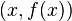 y
y 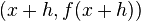 es
es .
.
 .
.
 existe en todos los puntos
existe en todos los puntos  , se puede definir la derivada de
, se puede definir la derivada de  como la función cuyo valor en cada punto
como la función cuyo valor en cada punto  es la derivada de
es la derivada de  en
en  .
.Puesto que sustituir
 por 0 produce una división por cero, calcular directamente la derivada puede no ser intuitivo. Una técnica posible consiste en operar en el numerador, de manera que se puede cancelar la
por 0 produce una división por cero, calcular directamente la derivada puede no ser intuitivo. Una técnica posible consiste en operar en el numerador, de manera que se puede cancelar la  del denominador. Y eso es posible fácilmente en los polinomios. Pero para muchas otras funciones el resultado es incierto. Afortunadamente, hay reglas generales que facilitan diferenciar la mayoría de las funciones simples.
del denominador. Y eso es posible fácilmente en los polinomios. Pero para muchas otras funciones el resultado es incierto. Afortunadamente, hay reglas generales que facilitan diferenciar la mayoría de las funciones simples.Sea
 una función continua, y
una función continua, y  su curva. Sea
su curva. Sea  la abscisa de un punto regular, es decir donde
la abscisa de un punto regular, es decir donde  no hace un ángulo. En el punto
no hace un ángulo. En el punto  de
de  se puede trazar la tangente a la curva. Su coeficiente director, o sea su pendiente, es
se puede trazar la tangente a la curva. Su coeficiente director, o sea su pendiente, es  , el número derivado de
, el número derivado de  en
en  .
.La función
 es la derivada de
es la derivada de  .
.
 , se puede saber a qué ritmo crece o decrece la función. El signo de
, se puede saber a qué ritmo crece o decrece la función. El signo de  determina en función
determina en función  (si crece o no).
(si crece o no).
 es creciente, las tangentes apuntan hacia arriba (mirando de izquierda a derecha), y por lo tanto
es creciente, las tangentes apuntan hacia arriba (mirando de izquierda a derecha), y por lo tanto  es positiva, como en el punto
es positiva, como en el punto  (
( ), mientras que donde
), mientras que donde  es decreciente, las tangentes apuntan hacia abajo y
es decreciente, las tangentes apuntan hacia abajo y  es negativa, como en el punto
es negativa, como en el punto 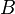 (
( ). En los puntos
). En los puntos  y
y  , que son máximo y mínimo local, la tangente es horizontal, luego
, que son máximo y mínimo local, la tangente es horizontal, luego  .
.La función derivada se puede calcular sin dibujar la curva de f. En efecto, gracias a una propiedad geométrica de la tangente, se tiene la fórmula:
[editar] Lista de derivadas de funciones elementales
En las fórmulas siguientes se considera que :
:[editar] Ejemplo
Sea la función
la función  , definida sobre el conjunto de los números reales (denotado por
, definida sobre el conjunto de los números reales (denotado por  ). Para conocer sus variaciones se observa su derivada:
). Para conocer sus variaciones se observa su derivada: , se tiene que factorizar:
, se tiene que factorizar:También se observa su segunda derivada:
- f''(x) = 12x − 18
 y
y 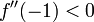 entonces
entonces  tiene un máximo local en -1 y su valor es
tiene un máximo local en -1 y su valor es  .
.Dado que
 y
y  entonces
entonces  tiene un mínimo local en 4 y su valor es
tiene un mínimo local en 4 y su valor es  .
.Nótese que la derivada es diferenciable en todo su dominio y hay exactamente 2 valores de x tales que
 , los cuales son
, los cuales son  y
y  , tomando en cuenta el teorema del valor medio y que
, tomando en cuenta el teorema del valor medio y que 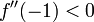 entonces la derivada es negativa en el intervalo
entonces la derivada es negativa en el intervalo  por lo tanto la función es decreciente en el intervalo
por lo tanto la función es decreciente en el intervalo ![[-1, 4]\,](http://upload.wikimedia.org/math/6/1/1/611de38c8dc92e6538c2915ff74ff16b.png) .
.Al ser una función basada en un polinomio cúbico no está acotada ni por arriba ni por abajo y como su derivada es una función cuadrática entonces no tiene más de 2 puntos con derivada igual a cero, por tanto la función es creciente en el intervalo
 y en el intervalo
y en el intervalo ![(-\infty, -1]\,](http://upload.wikimedia.org/math/0/8/0/0802ed6e9c23e30f050dbb8c9d7f296a.png)
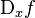 o
o 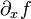 {Notaciones de
{Notaciones de 









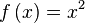


















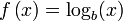
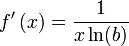


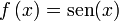



























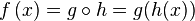
 (
(
