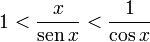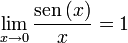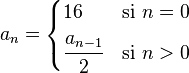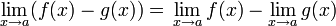Buscar este blog

limites

En matemática, el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.










Definición rigurosa
Informalmente, se dice que el límite de la función f(x) es L cuando x tiende a c, y se escribe:
\lim_{x\to c} \, \, f(x) = L
si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee. Formalmente, utilizando términos lógico-matemáticos:
\begin{array}{l} \underset {x\to c}{\lim} \, \, f(x) = L \iff \forall \varepsilon > 0 \ \ \exists \ \delta > 0 / \\ 0<|x-c|<\delta \longrightarrow |f(x)-L|<\epsilon \end{array}
Esta definición se denomina frecuentemente definición épsilon-delta de límite, y se lee como:
"El límite cuando x tiende a c existe si y sólo si para todo número real ε mayor que cero existe un número real δ mayor que cero tal que si la distancia entre x y c (x no es igual a c) es menor que δ, entonces la distancia entre la imagen de x y L es menor que ε unidades".

[editar] Límites notables

Como ejemplo de límites notables tenemos los siguientes límites de funciones, que proveen resultados muy interesantes.

[editar] Demostración

Para demostrar, por ejemplo, el segundo de estos límites, se utilizará la inecuación sen(x) < x < tan(x) en el intervalo (0,π/2), que relaciona x con las funciones seno y tangente. Luego dividimos por sen(x), obteniendo:
1 < \frac{x}{\operatorname{sen\,}x} < \frac{1}{\cos x}
Invirtiendo los términos de la inecuación y cambiando los signos de desigualdad:
\cos x < \frac{\operatorname{sen\,} x}{x} < 1
Calculando el límite cuando x tiende a 0:
\lim_{x\to 0} \cos x < \lim_{x\to 0} \frac{\operatorname{sen\,} x}{x} < \lim_{x\to 0} 1
Lo que es igual a:
1 < \lim_{x\to 0} \frac{\operatorname{sen\,} x}{x} < 1
Aplicando el teorema del sándwich o teorema de estricción, el límite necesariamente vale 1:
\lim_{x\to 0}\frac{\operatorname{sen\,}(x)}{x}=1
El tercero de los límites se demuestra utilizando las propiedades de los límites y el valor obtenido en el límite anterior. Es decir:
{\lim_{x \to 0} \left (\frac {\tan x}{x} \right )} = {\lim_{x \to 0} \left (\frac {\operatorname{sen\,} x}{x} \right )} \cdot \lim_{x \to 0} \frac{1}{\cos x}= 1 \cdot 1 = 1
El límite que obtiene el número e se demuestra de manera análoga, desarrollando el binomio de Newton y aplicando el límite cuando x tiende a infinito.

[editar] Límite de una sucesión

a_{n} = \begin{cases} 16 & \mbox{si } n = 0 \\ \cfrac{a_{n-1}}{2} & \mbox{si } n > 0 \end{cases}
Artículo principal: Límite de una sucesión
La definición del límite matemático en el caso de una sucesión es muy parecida a la definición del límite de una función cuando x tiende a \infty. Decimos que la sucesión an tiende hasta su límite a, o que converge o es convergente (a a), lo que denotamos como:
\lim_{n\to\infty}a_n = a
si podemos encontrar un número N tal que todos los términos de la sucesión a a cuando n crece sin cota. Formalmente:
a_n \to a \Leftrightarrow \forall\epsilon>0, \exists N>0 : \forall n\ge N, |a_n - a|<\epsilon

[editar] Propiedades de los límites

[editar] Generales

Los límites, como otros entes matemáticos, cumplen las siguientes propiedades generales, que son usadas muchas veces para simplificar el cálculo de los mismos.
  • \lim_{x \to a} x = \, a \,
  • Límite por un escalar.
\lim_{x \to a} kf(x) =\, k\lim_{x \to a} f(x)\, donde k es un multiplicador escalar.
  • Límite de una suma.
\lim_{x \to a} (f(x) + g(x)) =\, \lim_{x \to a} f(x) + \lim_{x \to a} g(x)\,
  • Límite de una resta.
\lim_{x \to a} (f(x) - g(x)) =\, \lim_{x \to a} f(x) - \lim_{x \to a} g(x)\,
  • Límite de una multiplicación.
\lim_{x \to a} (f(x) \cdot g(x)) =\, \lim_{x \to a} f(x) \cdot \lim_{x \to a} g(x)\,
  • Límite de una división.
\underset {x \to a} {\lim} \; \frac {f(x)}{g(x)} = \frac {\underset {x \to a} {\lim} \; f(x)} {\underset {x \to a} {\lim} \; g(x)} \quad \mathrm{si}\ \lim_{x \to a} g(x) \ne 0

[editar] Indeterminaciones

Hay límites que evaluándolos directamente, se obtiene alguna de las siguientes expresiones:
\infty - \infty , \quad \frac{\infty}{\infty} , \quad \infty \cdot 0 , \quad \frac{0}{0} , \quad \infty ^0 , \quad 1^\infty , \quad 0^0
A estas expresiones se les denomina indeterminaciones, ya que, a simple vista, no está claro cual puede ser el límite (si es que existe). Por ejemplo, en la segunda de estas ecuaciones, el límite pudiese valer 0, 1 o infinito. En algunos casos, simplificando las expresiones u obteniendo expresiones equivalentes a las iniciales, mediante racionalización o factorización se puede resolver la indeterminación y calcular el límite. En otros casos, se requerirá el uso de otras herramientas más potentes como pueden ser las desigualdades o la regla de L'Hopital.
Un ejemplo de indeterminación del tipo \textstyle \frac{0}{0} es la que se da en estos tres casos, y en cada caso (tras simplificar), se obtiene un límite distinto :
\lim_{t\rightarrow 0}\frac{t}{t^2}=\frac{0}{0} \quad \xrightarrow[\mathrm{simplificando}]{} \quad \lim_{t\rightarrow 0}\frac{1}{t} = \infty
\lim_{t\rightarrow 0}\frac{t}{t}=\frac{0}{0} \quad \xrightarrow[\mathrm{simplificando}]{} \quad \lim_{t\rightarrow 0} 1 =1
\lim_{t\rightarrow 0}\frac{t^2}{t}=\frac{0}{0} \quad \xrightarrow[\mathrm{simplificando}]{} \quad \lim_{t\rightarrow 0} {t} = 0
Límites laterales
Límite de f(x) en el punto a por la derecha :
limx->a+f(x)=b <=> para todo ε > 0 existe δ > 0 / para todo x perteneciente a (a,a + δ) |f(x) - b| < ε. Límite de f(x) en el punto a por la izquierda :
limx->a-f(x)=b <=> para todo ε > 0 existe δ > 0 / para todo x perteneciente a (a - δ,a) |f(x) - b| < ε.
Nota: x->a+ indica que x tiende a a por la derecha, es decir que x pertenece al entorno (a,a + δ).
x->a- indica que x tiende a a por la izquierda, es decir que x pertenece al entorno (a - δ,a).
A veces las funciones son discontinuas o no están definidas en un punto a, pero son continuas a uno y otro lado. En estos casos, el límite por la izquierda puede ser distinto del límite por la derecha.
Teorema Existe el límite finito de una función <=> los límites laterales son iguales.
H) limx->af(x)=b T) limx->a+f(x) = limx->a-f(x) = b
Demostración: Directo: limx->af(x)=b => (por def. de límite) para todo ε > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) pertenece al Eb,ε.
=> para todo ε > 0 existe δ > 0 / para todo x perteneciente a (a - δ,a) f(x) pertenece al Eb,ε => (por def. de límites laterales) limx->a-f(x)=b.
y para todo ε > 0 existe δ > 0 / para todo x perteneciente a (a,a + δ) f(x) pertenece al Eb,ε => (por def. de límites laterales) limx->a+f(x)=b.
Recíproco: limx->a+f(x)=b => (por def. de límites laterales) para todo ε > 0 existe δ1 > 0 / para todo x perteneciente a (a,a + δ1) f(x) pertenece al Eb,ε.
limx->a-f(x)=b => (por def. de límites laterales) para todo ε > 0 existe δ2 > 0 / para todo x perteneciente a (a - δ2,a) f(x) pertenece al Eb,ε.
Sea δ = min {δ1,δ2}
Para todo x perteneciente a E*a,δ f(x) pertenece al Eb,ε.
=> (por def. de límite) limx->af(x) = b.
Ejemplo: en la función del ejemplo anterior, no existe limx->2f(x), pues limx->2-f(x) ≠ limx->2+f(x).
Teorema Conservación del signo Para valores de x suficientemente próximos al valor de tendencia, la función tiene el mismo signo que su límite.
H) limx->af(x)=b > 0 T) Existe δ > 0 / para todo x perteneciente al E*a,δ f(x) > 0
Demostración: limx->af(x)=b => (por def. de límite) para todo ε > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) pertenece al Eb,ε. Es decir, b - ε < f(x) < b + ε.
Consideremos ε < b => 0 < b - ε < f(x) => f(x) > 0.
Así, basta considerar un ε menor que b, para tener un entorno de a donde f(x) es mayor que 0
Suscribirse a: Entradas (Atom)